Bridging Evolutionary Multiobjective Optimization
and GPU Acceleration via Tensorization
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
With the continuous rise in demand for complex optimization solutions across domains such as engineering design and energy management, evolutionary multiobjective optimization (EMO) algorithms have garnered widespread attention due to their robust capabilities in solving multiobjective problems. However, as optimization tasks grow in scale and complexity, traditional CPU-based EMO algorithms encounter significant performance bottlenecks.
To address this limitation, the EvoX team proposed to parallelize EMO algorithms on GPUs via the tensorization methodology. Leveraging this method, they have successfully designed and implemented several GPU-accelerated EMO algorithms. Furthermore, the team developed "MoRobtrol", a benchmark suite for multiobjective robot control built on the Brax physics engine, aimed at systematically evaluating the performance of GPU-accelerated EMO algorithms.
Based on these research advancements, the EvoX team has released EvoMO, a high-performance GPU-accelerated EMO algorithm library. The corresponding source code is publicly available on GitHub: https://github.com/EMl-Group/evomo
Tensorization Methodology
In the field of computational optimization, a tensor refers to a multi-dimensional array data structure capable of representing scalars, vectors, matrices, and higher-order data. Tensorization is the process of converting data structures and operations within an algorithm into tensor form, enabling the algorithm to fully leverage the parallel computing capabilities of GPUs.
In EMO algorithms, all key data structures can be expressed in a tensorized format. The individuals in a population can be represented by a solution tensor X, where each row vector corresponds to an individual. The objective function values form an objective tensor F. Additionally, auxiliary data structures such as reference vectors and weight vectors can be expressed as tensors R and W, respectively. This unified tensor representation enables population-level operations at the representation level, laying a solid foundation for large-scale parallel computation.
The tensorization of EMO algorithm operations is crucial for enhancing computational efficiency and can be divided into two layers: basic tensor operations and control flow tensorization. Basic tensor operations constitute the core of the tensorized implementation of EMO algorithms, as detailed in Table I.
Table I:Basic Tensor Operations

Control flow tensorization replaces traditional loop and conditional logic with parallelizable tensor operations. For example, for/while loops can be transformed into batched operations using broadcasting mechanisms or higher-order functions such as vmap. Similarly, if-else conditionals can be replaced by masking techniques, where logical conditions are encoded as Boolean tensors, enabling flexible switching between different computation paths.
Compared to traditional EMO algorithm implementations, the tensorization approach offers significant advantages. First, it provides greater flexibility, naturally handling multi-dimensional data, whereas conventional methods are often restricted to two-dimensional matrix operations. Second, tensorization significantly improves computational efficiency through parallel execution, avoiding the overhead associated with explicit loops and conditional branches. Lastly, it simplifies the code structure, resulting in more concise and maintainable programs.
As illustrated in Fig. 1, for instance, the traditional implementation of Pareto dominance checking relies on nested loops to perform element-wise comparisons. In contrast, the tensorized version achieves the same functionality through broadcasting and masking operations, enabling parallel evaluation. This not only reduces code complexity but also dramatically improves runtime performance.

Fig.1: Comparison between conventional and tensor-based implementations of Pareto dominance detection.
From a deeper perspective, tensorization is well-suited for GPU acceleration because GPUs possess a large number of parallel cores, and their single-instruction multiple-thread (SIMT) architecture aligns naturally with tensor computations, particularly excelling in matrix operations. Dedicated hardware such as NVIDIA's Tensor Cores further enhances the throughput of tensor operations. In general, algorithms that exhibit high parallelism, contain independent computational tasks, and have minimal conditional branching are more amenable to tensorization. For algorithms like MOEA/D, which involve sequential dependencies, the inherent structure poses challenges to direct tensorization. However, through structural refactoring and decoupling of critical computations, it is still possible to achieve effective parallel acceleration.
Application Example of Algorithm Tensorization
Based on the tensorized representation methodology, the EvoX team has designed and implemented tensorized versions of three classical EMO algorithms: the dominance-based NSGA-III, the decomposition-based MOEA/D, and the indicator-based HypE. The following section provides a detailed explanation using MOEA/D as an example. Tensorized implementations of NSGA-III and HypE can be found in the referenced paper.
As illustrated in Fig. 2, the traditional MOEA/D decomposes a multiobjective problem into multiple subproblems, each of which is optimized independently. The algorithm comprises four core steps: crossover and mutation, fitness evaluation, ideal point update, and neighborhood update. These steps are executed sequentially for each individual within a single loop. This sequential processing leads to substantial computational overhead when dealing with large populations, as each individual must complete all steps in order, limiting the potential benefits of GPU acceleration. In particular, the neighborhood update relies on interactions between individuals, which further complicates parallelization.

Fig.2: Pseudocode of MOEA/D
To address the issue of sequential dependencies in traditional MOEA/D, the team introduced a tensorized representation method within the internal loop of environmental selection. By decoupling crossover and mutation, fitness evaluation, ideal point update, and neighborhood update, these components are treated as independent operations. This enables parallel processing of all individuals, leading to the construction of a tensorized MOEA/D algorithm, referred to as TensorMOEA/D. In this algorithm, environmental selection is divided into two main stages: comparison and population update, and elite solution selection. These two stages are primarily tensorized through two applications of the vmap operation. The detailed process is illustrated in Fig. 3.
![]()
Fig.3: Overview of the environmental selection in the TensorMOEA/D algorithm. Left: Pseudocode of the algorithm. Right: Tensor dataflow of module (1) and module (2). The upper part of the right Fig. shows the overall tensor dataflow for modules (1) and (2), while the lower part presents the batch calculation tensor dataflow, with module (1) on the left and module (2) on the right.
To gain a more comprehensive understanding of the value of tensorization in EMO algorithms, it can be summarized from three perspectives. First, tensorization enables a direct transformation from mathematical formulations to efficient code, narrowing the gap between algorithm design and implementation. For example, Fig. 4 illustrates how the tensorized non-dominated sorting procedure can be translated directly from pseudocode into Python code. Second, tensorization significantly simplifies the code structure by unifying population-level operations into a single tensor representation. This reduces the reliance on loops and conditional statements, thereby improving code readability and maintainability. Third, tensorization enhances the reproducibility of algorithms. Its structured representation facilitates comparative testing and consistent reproduction of results.

Fig.4: he seamless transformation of the tensorized non-dominated sorting from pseudocode (Left) to Python code (Right).
Performance Demonstration
To evaluate the performance of GPU-accelerated multiobjective optimization algorithms, the EvoX team systematically conducted three categories of experiments, focusing on computational acceleration, numerical optimization performance, and effectiveness in multiobjective robotic control tasks.
Computational Acceleration Performance:
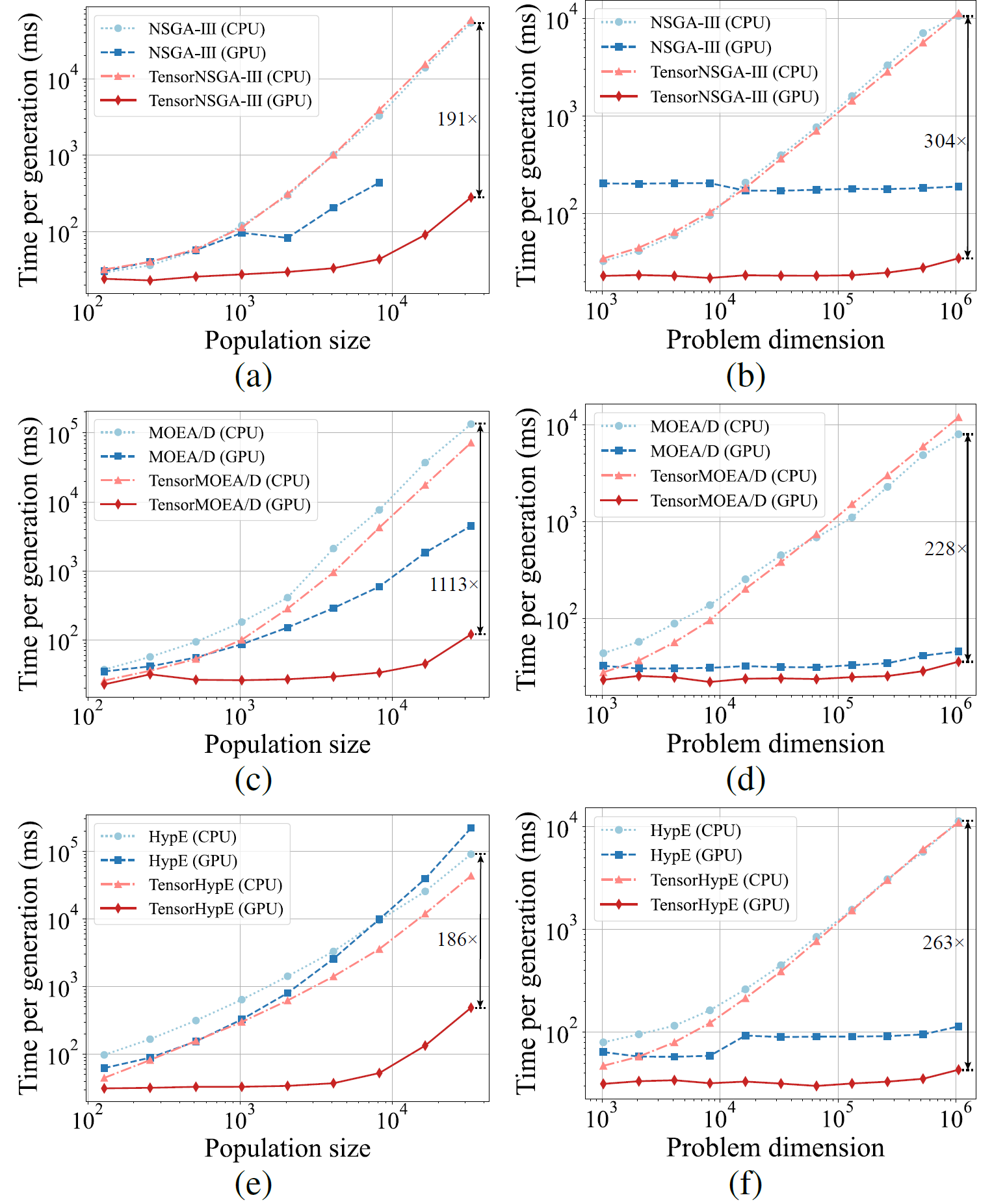
Fig.5: Comparative acceleration performance of NSGA-III, MOEA/D, and HypE with their tensorized counterparts on CPU and GPU platforms across varying population sizes and problem dimension.
Experimental results show that TensorNSGA-III, TensorMOEA/D, and TensorHypE achieve significantly higher execution speeds on GPUs compared to their non-tensorized CPU-based counterparts. As the population size and problem dimensionality increase, the maximum observed speedup reaches up to 1113×. The tensorized algorithms demonstrate excellent scalability and stability when handling large-scale computational tasks—their runtime increases only marginally, while maintaining consistently high performance. These findings highlight the substantial advantages of tensorization for GPU acceleration in multiobjective optimization.
Performance on the LSMOP Test Suite:
Table II:Statistical Results (Mean and Standard Deviation) of the IGD and Runtime (s) for Non-Tensorized and Tensorized EMO Algorithms in LSMOP1--LSMOP9. All Experiments Are on an RTX 4090 GPU and the Best Results Are Highlighted.
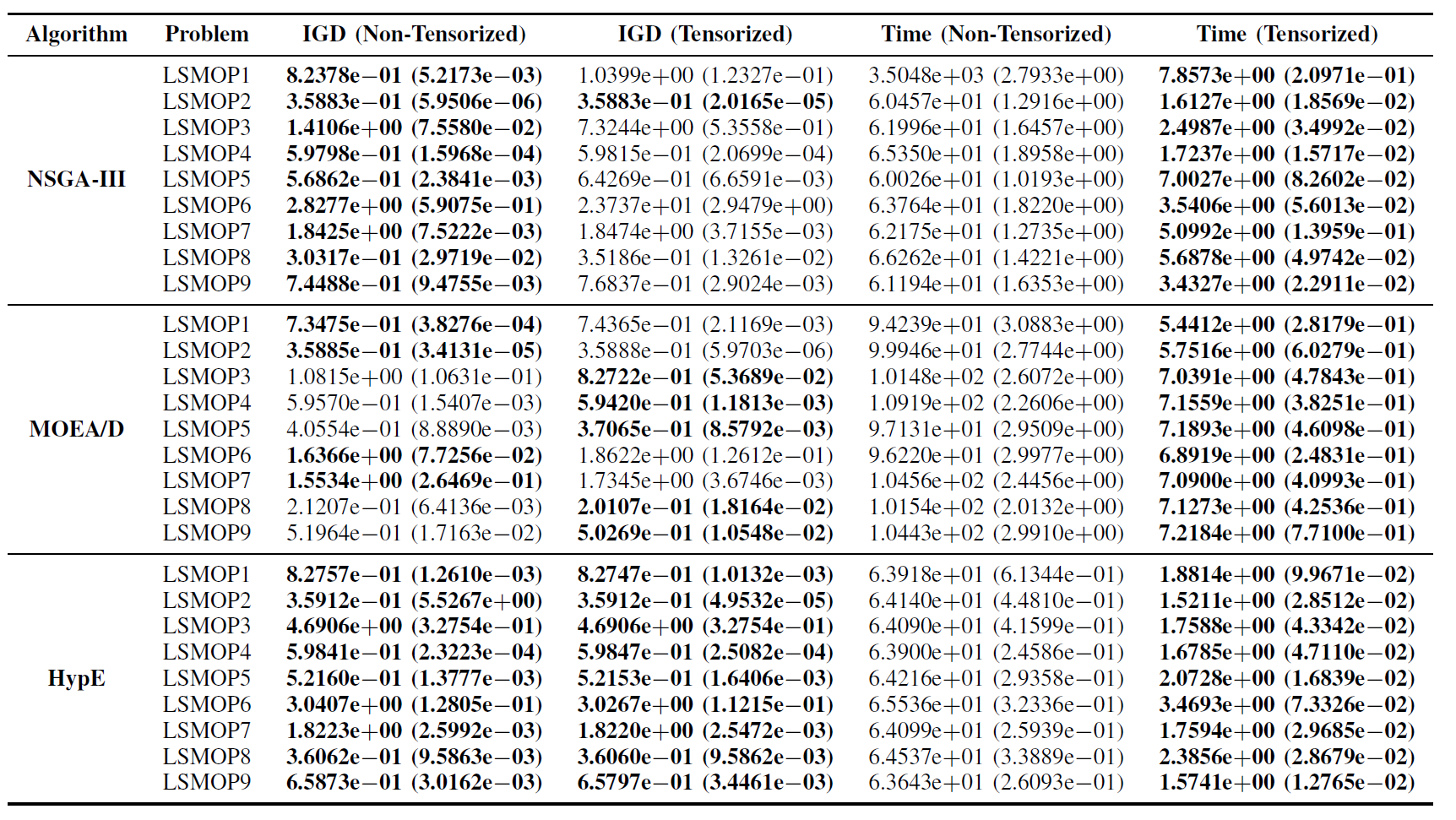
Experimental results indicate that the GPU-accelerated EMO algorithms based on tensorized representations significantly improve computational efficiency while maintaining, and in some cases even surpassing, the optimization accuracy of their original counterparts.
Multiobjective Robot Control Tasks:
To comprehensively evaluate the practical performance of GPU-accelerated EMO algorithms, the team developed a benchmark suite named MoRobtrol for multiobjective robot control. The tasks included in this suite are listed in Table III.
Table III:Overview of Multiobjective Robot Control Problems in the Proposed MoRobtrol Benchmark Test Suite
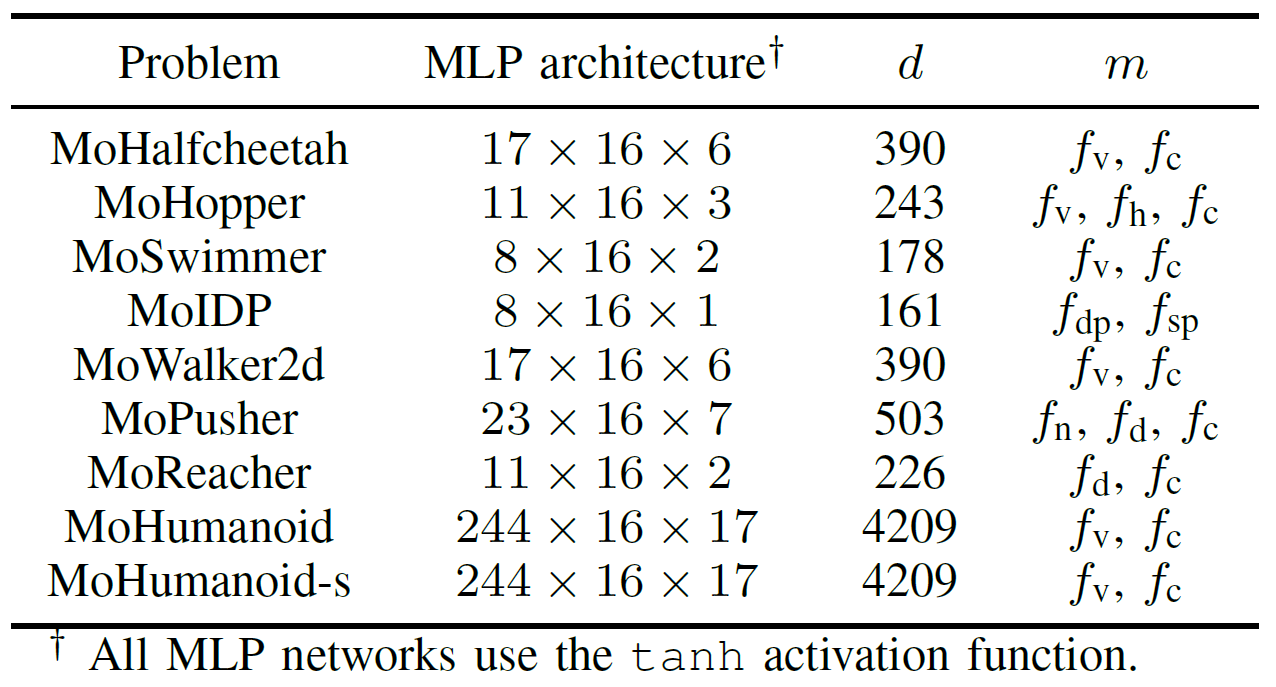
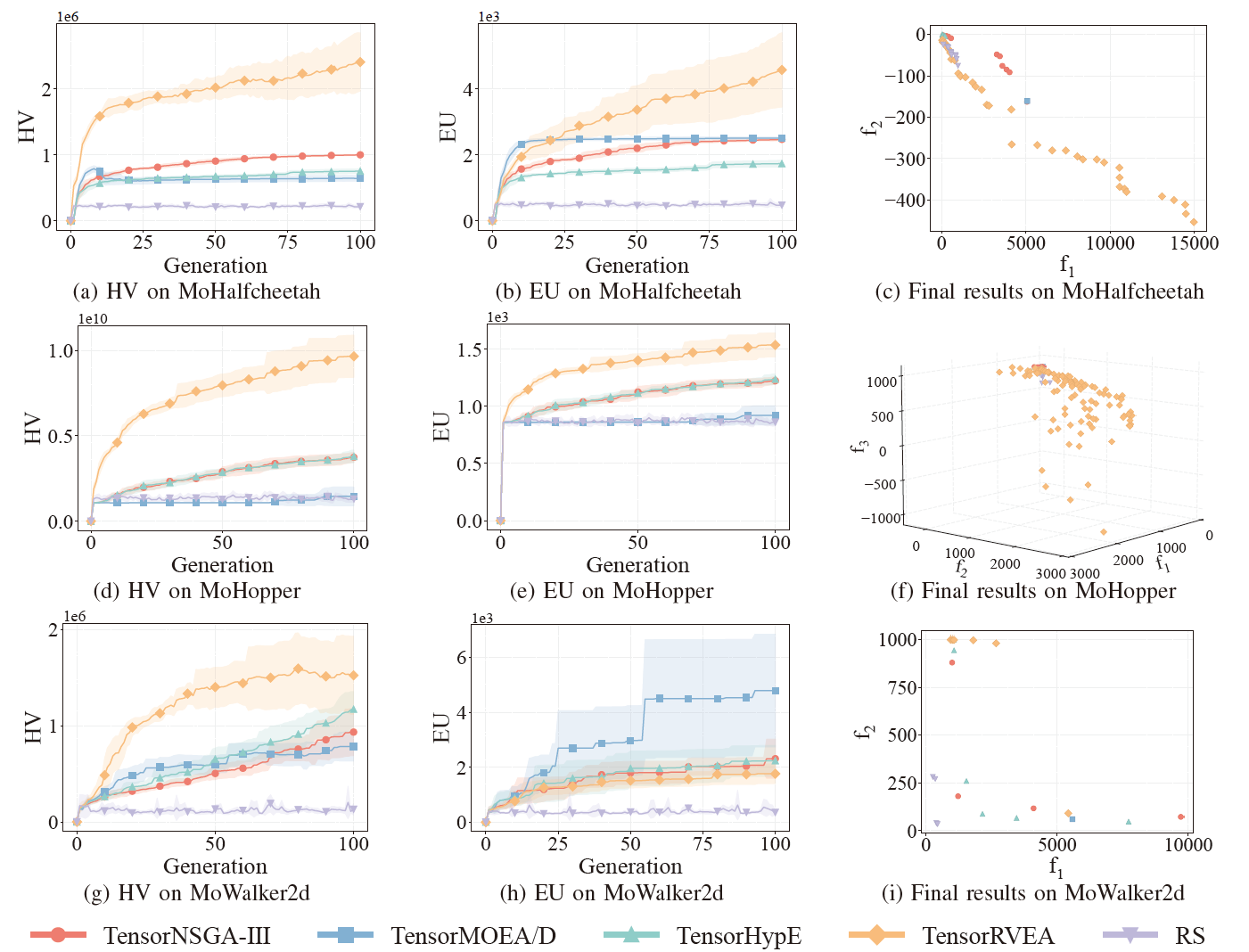
Fig.6: Comparative performance (HV, EU, and visualization of final results) of TensorNSGA-III, TensorMOEA/D, TensorHypE,TensorRVEA, and random search (RS) across varying problems: MoHalfcheetah (390D), MoHopper (243D), and MoWalker2d (390D). Note: Higher values for all metrics indicate better performance.
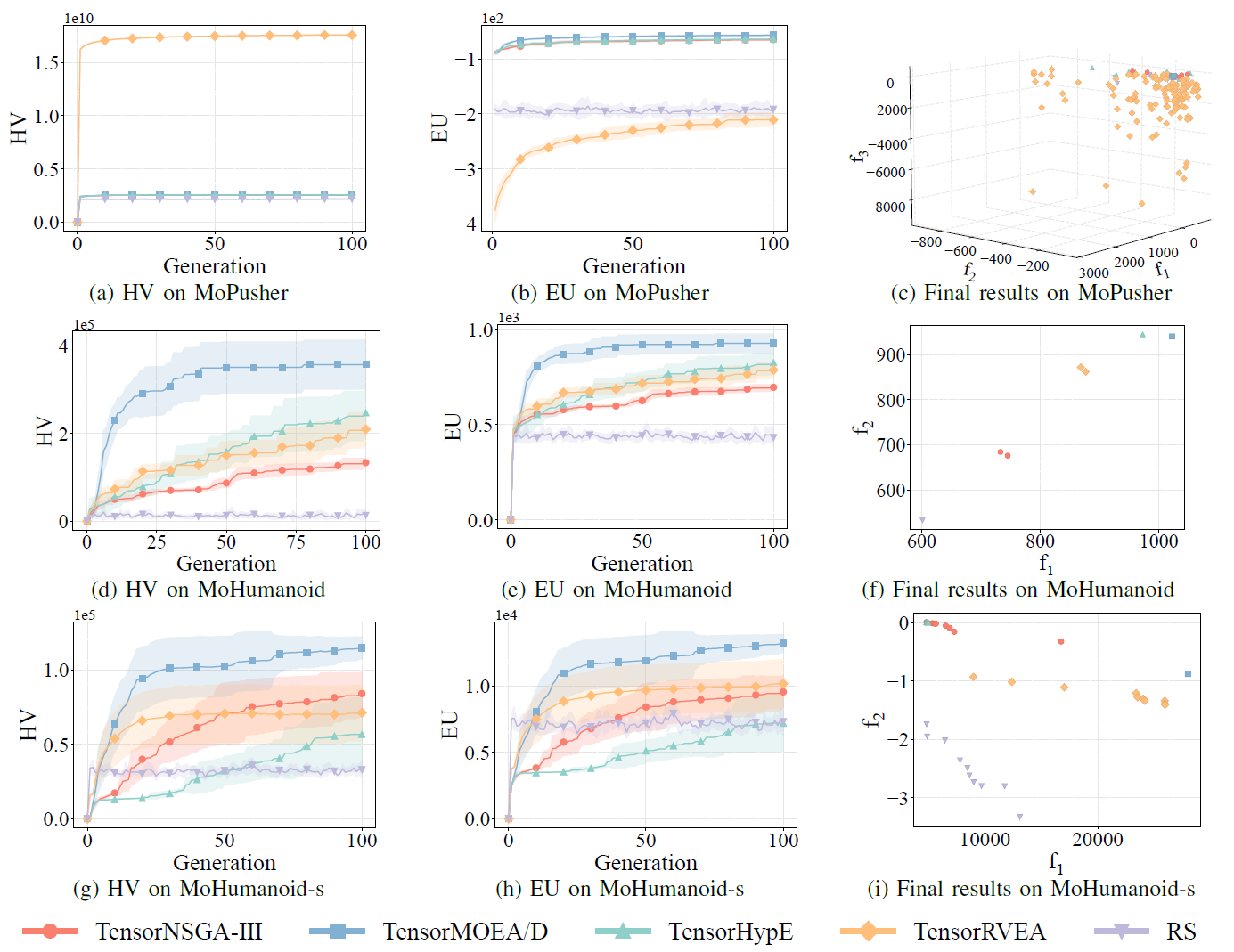
Fig.7: Comparative performance (HV, EU, and visualization of final results) of TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA, and random search (RS) across varying problems: MoPusher (503D), MoHumanoid (4209D), and MoHumanoid-s (4209D). Note: Higher values for all metrics indicate better performance.
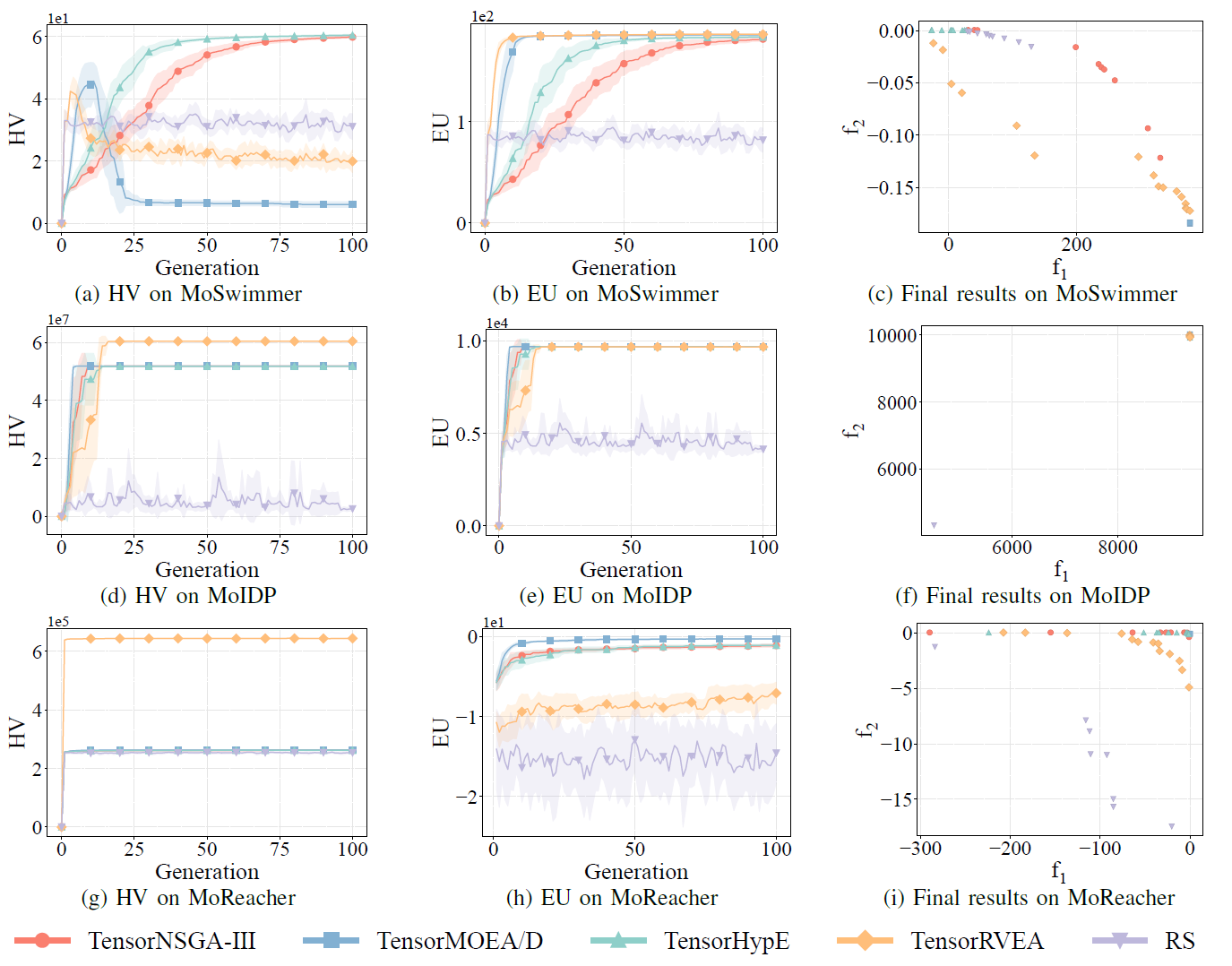
Fig.8: Comparative performance (HV, EU, and visualization of final results) of TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA, and random search (RS) across varying problems: MoSwimmer (178D), MoIDP (161D), and MoReacher (226D). Note: Higher values for all metrics indicate better performance.
The experiments compared the performance of TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA, and Random Search (RS) within the MoRobtrol benchmark. The results show that TensorRVEA achieved the best overall performance, obtaining the highest HV values and demonstrating good solution diversity across multiple environments. TensorMOEA/D exhibited strong adaptability in large-scale tasks, particularly excelling in preference consistency of solutions. TensorNSGA-III and TensorHypE showed similar performance and were competitive on several tasks. Overall, tensorized decomposition-based algorithms demonstrated superior advantages in solving large-scale and complex problems.
Conclusion and Future Work
This study proposes a tensorized representation methodology to address the limitations of traditional CPU-based EMO algorithms in terms of computational efficiency and scalability. The approach has been applied to several representative algorithms, including NSGA-III, MOEA/D, and HypE, achieving significant performance improvements on GPUs while maintaining solution quality. To validate its practical applicability, the team also developed MoRobtrol, a multiobjective robotic control benchmark suite that reformulates robotic control tasks in physics simulation environments as multiobjective optimization problems. The results demonstrate the potential of tensorized algorithms in computationally intensive scenarios such as embodied intelligence. Although the tensorization method has substantially improved algorithmic efficiency, there remains room for further enhancement. Future directions include improving core operators such as non-dominated sorting, designing new tensorized operations for multi-GPU systems, and integrating large-scale data and deep learning techniques to further enhance performance on large-scale optimization problems.
Open Source Code / Community Resources
Paper:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
Upstream Project (EvoX):
https://github.com/EMI-Group/evox
QQ Group: 297969717


